Linear Algebra Package (LAPACK)

​LAPACK website ​List of subroutine

Many routines for linear algebra. Typical name: XYYZZZ

• X is precision
• YY is type of matrix,
  • e.g. GE (general), GB (general banded), GT (general tridiagonal)

• ZZZ is type of operation,
  • e.g. SV (solve system), SVX (solve system expert), EV (eigenvalues, vectors), SVD (singularvalues, vectors)

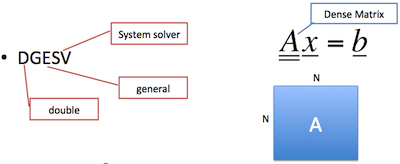
General Dense Matrix System Solver

Ex: DGESV( N, NRHS, A, LDA, IPIV, B, LDB, INFO )

DGESV computes the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = P * L * U, where P is a permutation matrix, L is unit lower triangular, and U is upper triangular. The factored form of A is then used to solve the system of equations A * X = B.

Example Codes

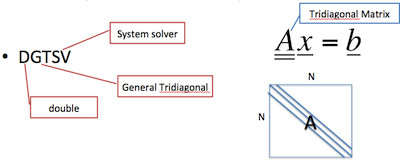
Tri-diagonal Matrix System Solver

Ex:DGTSV( N, NRHS, DL, D, DU, B, LDB, INFO )

DGTSV solves the equation A*X = B, where A is an n by n tridiagonal matrix, by Gaussian elimination with partial pivoting. Note that the equation A'*X = B may be solved by interchanging the order of the arguments DU and DL.

Example Codes

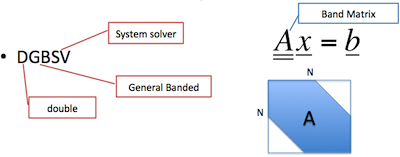
Band Matrix System Solver

Ex: DGBSV( N, KL, KU, NRHS, AB, LDAB, IPIV, B, LDB, INFO )

DGBSV computes the solution to a real system of linear equations A * X = B, where A is a band matrix of order N with KL subdiagonals and KU superdiagonals, and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = L * U, where L is a product of permutation and unit lower triangular matrices with KL subdiagonals, and U is upper triangular with KL+KU superdiagonals. The factored form of A is then used to solve the system of equations A * X = B.

Band Storage Scheme

Example Codes